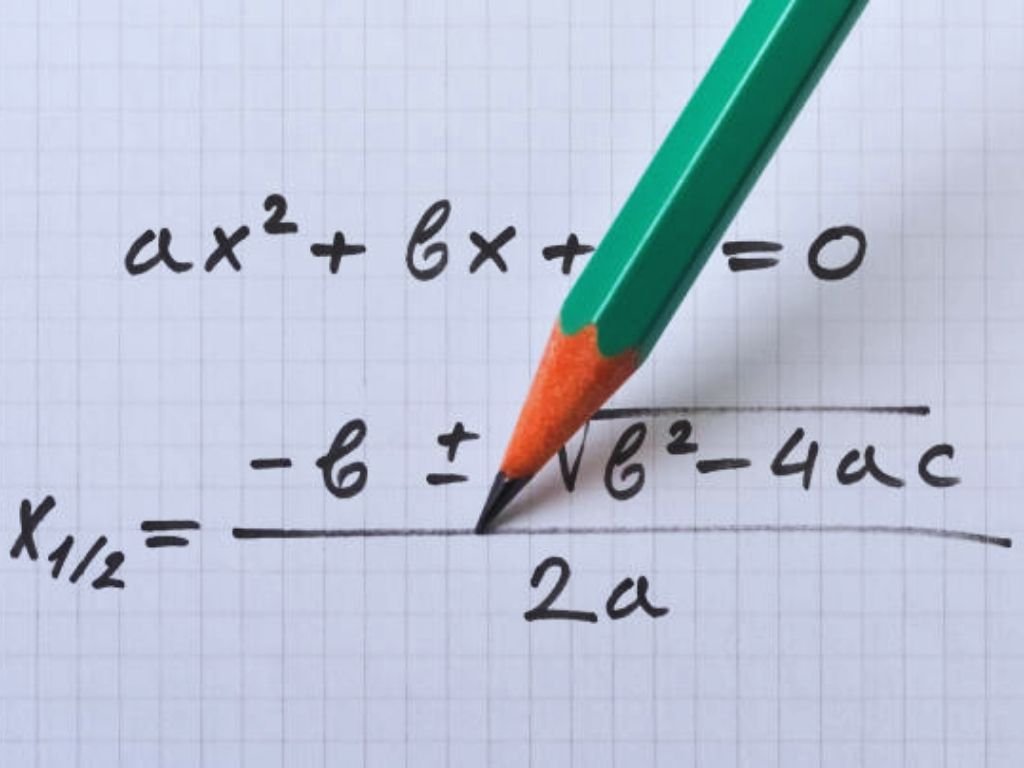Factorization Method Class 10th

Introduction

In the Factorization Method, we factorize the quadratic equation and put each factor equal to zero and then find the values of x. These values of x are the solution of the quadratic equation and are called the roots of the quadratic equation.

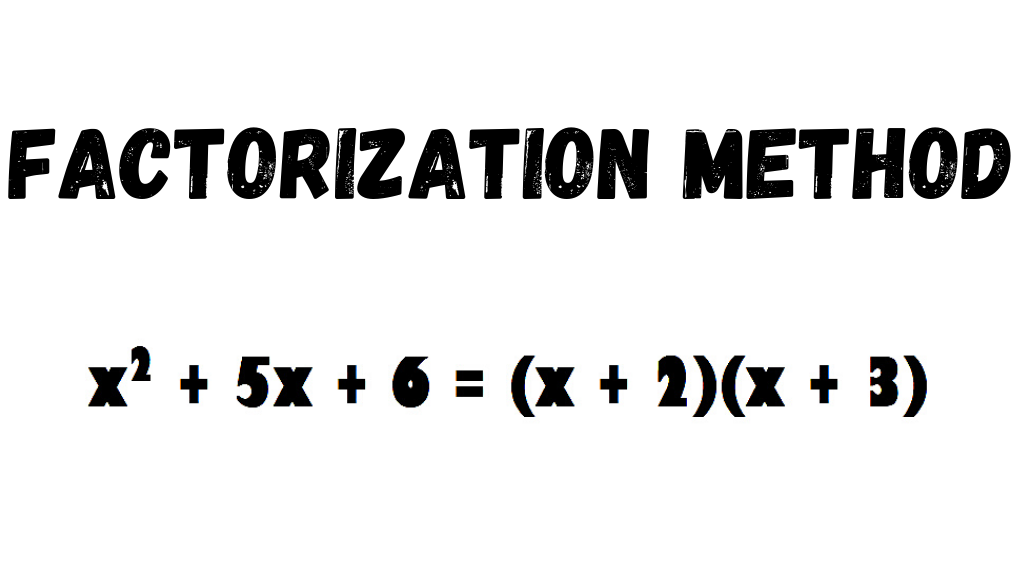
This can be understood by the following examples.

Examples

Example – 1) Find the roots of the quadratic equation x² + 5x + 6 = 0 by factorization method.

Solution – given equation   x² + 5x + 6 = 0

Step (1) Comparing the equation with the standard form ax² + bx + c = 0

a = 1, b = 5, c = 6

We take      a⨯c = 1⨯6 = 6    and      b = 5

Step (2) Now, we have to take two numeric values so that their sum should be equal to b i.e., 5 and their multiplication should be equal to a⨯c i.e., 6. So, we take the numbers 2 and 3.

Note – if it is difficult to find the two numeric values, we can factorize the term a⨯c and make pair to get it easily. 

Step (3) Now check

2+3 = 5 and 2⨯3 = 6 (these values satisfy)

Step (4) Now, break the middle term of equation x² + 5x + 6 with the help of the above sum 2+3 = 5

x² + (2+3)x + 6 = 0

x² + 2x + 3x + 6 = 0

Step (5) Now take common terms out from the first two terms and last two terms.

x(x + 2) + 3(x+2) = 0

(x+2) is again a common term so,

(x+2) (x+3) = 0

Step (6) Now, by putting each factor equal to zero.

(x+2) = 0   and    (x+3) = 0

x = -2    and         x = -3 Ans.

Both the values of x are the solution of the given quadratic equation and are called the roots of this equation.

We can check our answer by putting the values of x in the given quadratic equation.

x² + 5x + 6 = 0

at x = -2,                                                          

(-2)² + 5(-2) + 6 = 0                                         

4 – 10 + 6 = 0                                                  

– 6 + 6 = 0                                                         

0 = 0                                                                 

LHS = RHS                                                    

at x = -3,

(-3)² + 5(-3) + 6 = 0

9 – 15 + 6 = 0

– 6 + 6 = 0

0 = 0

LHS = RHS

At both values, LHS = RHS which means our answer is correct.

Example – 2) Find the roots of the quadratic equation 2x² – 5x + 3 = 0 by factorization method.

Solution – 2x² – 5x + 3 = 0             Here, a⨯c = 2⨯3 = 6 and b = -5

2x² – (2+3)x + 3 = 0                        two numeric values -2 and -3

2x² – 2x – 3x + 3 = 0                       -2⨯(-3) = 6 and -2 + (-3) = -2 – 3 = -5 

2x(x-1) -3(x-1) = 0

(x-1) (2x-3) = 0

(x-1) = 0   and   (2x-3) = 0

x = 1    and       x = 3/2     

Thus, the roots of the quadratic equation 2x² – 5x + 3 = 0 are x = 1 and x = 3/2.    Ans.

Factorization Method Class 10^th in Hindi

More About Factorization Method