Trigonometric Ratios of Some Specific Angles Class 10th

In Trigonometry, For all the trigonometric ratios we will find their values for some specific angles 0°, 30°, 45°, 60°, and 90°.

Trigonometric Ratios of Angle 0°

Let △ABC be a right-angled triangle in which ∠B is the right angle and ∠C is an acute angle ϴ. If the angle ϴ becomes 0° then line segment AC(Hypotenuse) will coincide with line segment BC(Base) and line segment AB(Perpendicular) will become 0. it means AB = 0 and AC = BC.

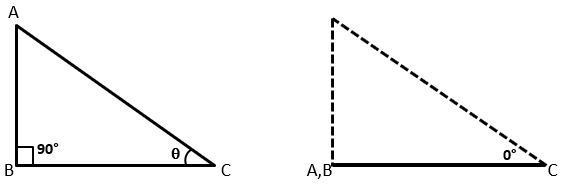
Thus, the values of trigonometric ratios for angle 0°

sin 0° = AB/AC = 0/AC = 0	cosec 0° = AC/AB = AC/0 = ∞ (infinitive)
cos 0° = BC/AC = BC/BC = 1	sec 0° = AC/BC = BC/BC = 1
tan 0° = AB/BC = 0/BC = 0	cot 0° = BC/AB = BC/0 = ∞ (infinitive)

Trigonometric Ratios of Angles 30° and 60°

Let △ABC be an equilateral triangle with each side 2a. Therefore AB=BC=CA=2a and ∠A=∠B=∠C=60°. AD is perpendicular on side BC from vertex A (AD ⊥ BC).

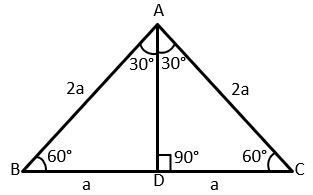
In △ABD and △ACD,

∠ADB = ∠ADC = 90°

AB = AC = 2a

AD = AD (Common side)

By RHS criterion, △ABD ≅ △ACD

Therefore, BD = CD = a and ∠BAD = ∠CAD = 30° (by CPCT)                       

In a right-angled triangle ABD

AB = 2a, BD = a

AD² = AB² – BD² (by Pythagoras theorem)                                                      

AD² = (2a)² – (a)² = 4a² – a²

AD = √3a² 

AD = a√3

Trigonometric ratios of angle 30°

sin 30° = BD/AB = a/2a = 1/2	cosec 30° = AB/BD = 2a/a = 2
cos 30° = AD/AB = a√3/2a = √3/2	sec 30° = AB/AD = 2a/a√3 = 2/√3
tan 30° = BD/AD = a/a√3 = 1/√3	cot 30° = AD/BD = a√3/a = √3

Now Trigonometric ratios of angle 60°

sin 60° = AD/AB = a√3/2a = √3/2	cosec 60° = AB/AD = 2a/a√3 = 2/√3
cos 60° = BD/AB = a/2a = 1/2	sec 60° = AB/BD = 2a/a = 2
tan 60° = AD/BD = a√3/a = √3	cot 60° = BD/AD = a/a√3 = 1/√3

Trigonometric Ratios of Angle 45°

Let △ABC be a right-angled triangle. In which ∠B is the right angle and ∠C = 45°.

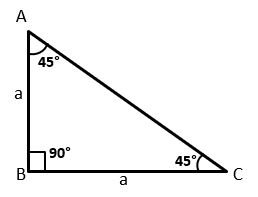
Now ∠A + ∠B + ∠C = 180°

∠A + 90° + 45° = 180°

∠A = 180° – 135°

∠A = 45° 

Since ∠A = ∠C

Therefore, AB = BC (opposite sides of equal angles are equal)

Let AB = BC = a

Then AC² = AB² + BC² (by Pythagoras theorem)

AC² = (a)² + (a)² = a² + a²

AC = √2a² = a√2

Thus, the values of trigonometric ratios for angle 45°

sin 45° = AB/AC = a/a√2 = 1/√2	cosec 45° = AC/AB = a√2/a = √2
cos 45° = BC/AC = a/a√2 = 1/√2	sec 45° = AC/BC = a√2/a = √2
tan 45° = AB/BC = a/a = 1	cot 45° = BC/AB = a/a = 1

Trigonometric Ratios of Angle 90°

Let △ABC be a right-angled triangle in which ∠B is the right angle and ∠C is an acute angle ϴ. If the angle ϴ becomes 90° then line segment AC(Hypotenuse) will coincide with line segment AB(Perpendicular) and line segment BC(Base) will become 0. it means BC = 0 and AC = AB.

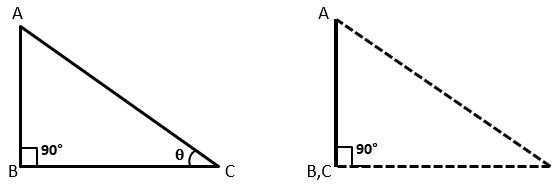
Thus, the values of trigonometric ratios for angle 90°

sin 90° = AB/AC = AB/AB = 1	cosec 90° = AC/AB = AB/AB = 1
cos 90° = BC/AC = 0/AC = 0	sec 90° = AC/BC = AC/0 = ∞ (infinitive)
tan 90° = AB/BC = AB/0 = ∞ (infinitive)	cot 90° = BC/AB = 0/AB = 0

From all the above values if we make a table so all these values will be remembered easily.

Trigonometric Ratios∖Angles (ϴ) (in Degree)➡ ⬇	0°	30°	45°	60°	90°
sin ϴ	0	1/2	1/√2	√3/2	1
cos ϴ	1	√3/2	1/√2	1/2	0
tan ϴ	0	1/√3	1	√3	∞
cosec ϴ	∞	2	√2	2/√3	1
sec ϴ	1	2/√3	√2	2	∞
cot ϴ	∞	√3	1	1/√3	0

Steps to Remember the Table Quickly –

1) First of all, we have to write numbers 0, 1, 2, 3, and 4 for the angles 0°, 30°, 45°, 60°, and 90° respectively.

2) After that we shall divide each number by 4 as follows

0/4 = 0

1/4

2/4 = 1/2

3/4

4/4 = 1

3) Now we have the numbers 0, 1/4, 1/2, 3/4, and 1. We shall take the square root of these numbers.

√0 = 0

√1/4 = 1/2

√1/2 = 1/√2

√3/4 = √3/2

√1 = 1

These values are for sin ϴ.

4) By writing these values in the reverse order we shall get the values for cos ϴ.

Reverse order →

1

√3/2

1/√2

1/2

0

5) For tan ϴ, we shall divide the values of sin ϴ by values of cos ϴ because tan ϴ = sin ϴ/cos ϴ.

0/1 = 0

1/2 ∕ √3/2 = 1/√3

1/√2 ∕ 1/√2 = 1

√3/2 ∕ 1/2 = √3

1/0 = ∞ (infinite)

6) Now we shall take the reciprocal of the values of sin ϴ to get the values of cosec ϴ because cosec ϴ = 1/sin ϴ.

Reciprocal →

1/0 = ∞ (infinite)

1 ∕ 1/2 = 2

1 ∕ 1/√2 = √2

1 ∕ √3/2 = 2/√3

1/1 = 1

7) For sec ϴ, we shall write the values of cosec ϴ in the reverse order.

Reverse order →

1

2/√3

√2

2

∞ (infinite)

8) For cot ϴ, we shall take the reciprocal of the values of tan ϴ because cot ϴ = cos ϴ/sin ϴ.

Reciprocal →

1/0 = ∞ (infinite)

1 ∕ 1/√3 = √3

1/1 = 1

1/√3

0/1 = 0

Examples –

Example – 1) find the value of sin 60° cos 30° – sin 30° cos 60°.

Solution – sin 60° cos 30° – sin 30° cos 60°

(√3/2)⨯(√3/2) – (1/2)⨯(1/2) = 3/4 – 1/4 = 3-1/4 = 2/4 = 1/2 Ans. 

Example – 2) find the value of tan² 45° + sin² 30° – cos² 60°

Solution – tan² 45° + sin² 30° – cos² 60°

(1)² + (1/2)² – (1/2)² = 1 + 1/4 – 1/4 = 1 Ans.

Trigonometric Ratios of Some Specific Angles Class 10^th in Hindi

More About Trigonometric Ratios of Some Specific Angles