In this section, we shall study different mathematical operations on real numbers such as addition, subtraction, multiplication, and division. We know that rational numbers and irrational numbers are real numbers so we’ll apply operations on them.
For Rational Numbers
As we have learnt in previous classes, rational numbers satisfy the commutative, associative, and distributive properties of addition and multiplication. We also know that rational numbers are closed under addition, subtraction, multiplication, and division because if we add, subtract, multiply, or divide (except zero) two rational numbers, we always get a rational number.
Example – Add, subtract, multiply, and divide two rational numbers 2 and ¼.
Solution – Addition, 2 + ¼ = (2×4 + 1) / 4 = (8 + 1) / 4 = 9/4
Subtraction, 2 – ¼ = (2×4 – 1) / 4 = (8 – 1) / 4 = 7/4
Multiplication, 2 × ¼ = 2/4 = ½
Division, 2 ÷ ¼ = 2 × 4/1 = 8
We can see that 9/4, 7/4, ½, and 8 are also rational numbers. Ans.
For Irrational Numbers
Irrational numbers also satisfy the commutative, associative, and distributive law of addition and multiplication but irrational numbers are not closed under addition, subtraction, multiplication, and division because if we add, subtract, multiply, or divide two irrational numbers, we do not get always an irrational number.
Examples –
(1) Add two irrational numbers √5 and -√5.
Solution – (√5) + (-√5) = √5 – √5 = 0
(2) Subtract √2 from √2.
Solution – √2 – √2 = 0
(3) Multiply √6 and √6.
Solution – √6 × √6 = 6
(4) Divide √10 by √10.
Solution – √10 ÷ √10 = √10 / √10 = 1
We can see that 0, 0, 6, and 1 are rational numbers. Ans.
For Both Rational and Irrational Numbers
What happens when we apply mathematical operations between a rational number and an irrational number? Let us understand this with the help of some examples.
Examples –
(1) Add √3 and 4.
Solution – √3 + 4
We know that √3 is an irrational number because its decimal expansion is non-terminating non-recurring. Therefore, √3 + 4 will also be an irrational number. Ans.
(2) Subtract 2 from √7.
Solution – √7 – 2
Here, √7 is an irrational number because of non-terminating non-recurring decimal expansion. Therefore, √7 – 2 will also be an irrational number. Ans.
(3) Multiply √5 by 5.
Solution – √5×5 = 5√5
√5 is an irrational number. Therefore, 5√5 will also be an irrational number. Ans.
(4) Divide 9 by √8.
Solution – 9 ÷ √8 = 9/√8
9/√8 will be an irrational number because √8 is an irrational number. Ans.
In all the above examples, we get irrational numbers. Now, we add, subtract, multiply, divide, take square roots, and even nth roots of these irrational numbers, where n is any natural number. Let’s take some examples to understand.
Example (1) Add √3 + 8√2 and 5√3 – 3√2.
Solution – (√3 + 8√2) + (5√3 – 3√2)
(√3 + 5√3) + (8√2 – 3√2)
(1 + 5)√3 + (8 – 3)√2
6√3 + 5√2 Ans.
Example (2) Subtract 2√5 + 3√7 from 5√7 + 3√5.
Solution – (5√7 + 3√5) – (2√5 + 3√7)
5√7 + 3√5 – 2√5 – 3√7
(5√7 – 3√7) + (3√5 – 2√5)
(5 – 3)√7 + (3 – 2)√5
2√7 + √5 Ans.
Example (3) Multiply 10√2 by 3√2.
Solution – 10√2 × 3√2
10×3×√2×√2
30×2
60 Ans.
Example (4) Divide 9√15 by 3√12.
Solution – 9√15 ÷ 3√12
9√15 / 3√12
9×√3×√5 / 3×√4×√3
3√5 / 2 Ans.
The above explanation helps us to consider some true statements, which are as follows –
- The addition and subtraction of a rational number and an irrational number are always irrational.
- The multiplication and division of a non-zero (except zero) rational number with an irrational number are always irrational.
- The addition, subtraction, multiplication, and division of two irrational numbers may be rational or irrational.
- The addition, subtraction, multiplication, and division (except zero) of two rational numbers are always rational.
Square Root Operation on Real Numbers
For the natural number a, we can write, √a = b
Or we can write, b2 = a and b > 0.
The same definition can be applied to positive real numbers as well.
Let a be a real number and a > 0.
Then √a = b
Or we can write, b2 = a and b > 0.
Now, we find the square root of a positive real number geometrically. Let x be a positive real number and we find √x geometrically.
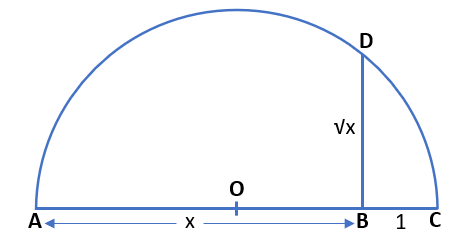
First, we draw a line segment AB of measure x units. After that, we take the C point such that BC = 1 unit. With the help of a compass and scale, we get the midpoint of AC which is point O. Taking point O as a centre and radius OA, we draw a semicircle. At point B, we draw a perpendicular BD which intersects the semicircle at point D.
Therefore, the perpendicular BD = √x.
This is the geometric way to find the square root of a positive real number.
We can also find how BD = √x. Again, using the above figure.
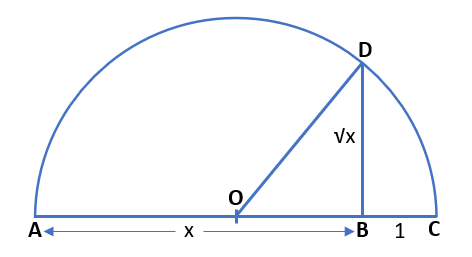
After joining OD, we can see that △OBD is a right-angled triangle. Also, the radius of the circle is (x+1)/2 units because the diameter is x+1 units.
Therefore, OA = OC = OD = (x+1)/2 units
Now, OB = OC – BC = (x+1)/2 – 1
OB = x + 1 – 2 / 2 = (x – 1)/2 units
Using Pythagoras’s theorem, in △OBD,
BD2 = OD2 – OB2
BD2 = {(x+1)/2}2 – {(x-1)/2}2
BD2 = (x+1)2/4 – (x-1)2/4
BD2 = (x2 + 2x + 1) – (x2 – 2x + 1) / 4
BD2 = x2 + 2x + 1 – x2 + 2x – 1 / 4
BD2 = 4x/4 = x
BD = √x
We get BD = √x by this geometric way and the above construction shows that √x exists for all real numbers where x > 0.
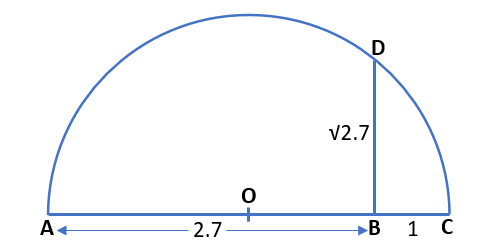
For example, if we find it for x = 2.7, i. e. we will find √2.7 geometrically.
Then we’ll draw AB = 2.7 units and mark a point C at a distance of 1 unit from point B. After that we’ll find the midpoint of AC with the help of a compass and scale and mark that point as O. Taking point O as a centre and radius OA, we draw a semicircle. Now, we’ll draw perpendicular on AC which is passing through point B and intersects the semicircle at point D. i.e. BD ⊥ AC.
Then BD = √2.7
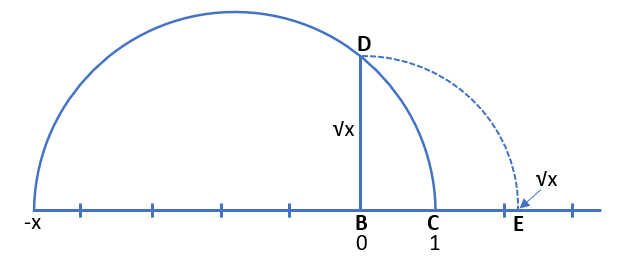
We can also find the position of √x on the number line. Let us assume BC as a number line and take B as 0, C as 1, and so on. With B as the centre, we draw an arc equal to BD which intersects the number line at point E. Then point E represents √x.
nth Roots of Real Numbers
We have an idea of square roots and cube roots as already studied in earlier classes. Let’s understand with the help of some examples.
1) √9 = 3
We know that 3 is the number whose square is 9.
Or we can write, 32 = 9
2) 3√8 = 2
We know that 2 is the number whose cube is 8.
Or we can write, 23 = 8
3) 4√81 = 3
We know that 3 is the number whose multiplication by itself four times is 81.
Or we can write, 34 = 81
4) 5√32 = 2
We know that 2 is the number whose multiplication by itself five times is 32.
Or we can write, 25 = 32
From these examples, we can define n√a for a real number a > 0 and a positive integer n.
Let a be a real number that a > 0 and n be a positive integer.
Then n√a = b
Or we can write, bn = a and b > 0.
Note – The symbol ‘√’ used in √9, 3√8, 5√32, n√a, etc. is called the radical sign.
Here are some identities which are related to square roots. Let a and b be two positive real numbers. Then
| (i) √ab = √a√b | (v) (a + √b)(a – √b) = (a)2 – (√b)2 = a2 – b |
| (ii) √a/b = √a / √b | (vi) (√a + √b)(√c + √d) = √ac + √ad + √bc + √bd |
| (iii) √a×√a = a | (vii) (√a + √b)2 = (√a)2 + 2√ab + (√b)2 = a + 2√ab + b |
| (iv) (√a + √b)(√a – √b) = (√a)2 – (√b)2 = a – b | (viii) (√a – √b)2 = (√a)2 – 2√ab + (√b)2 = a – 2√ab + b |
Some Examples
Example – Simplify the following expressions:
(1) (√2 + √3)(√2 – √3)
(2) (√5 + √2)(√3 + √7)
(3) (√7 + √2)2
(4) (8 – √3)(√2 + 1)
Solution – (1) (√2 + √3)(√2 – √3)
Using the identity, (√a + √b)(√a – √b) = (√a)2 – (√b)2 = a – b
(√2)2 – (√3)2 = 2 – 3 = -1 Ans.
(2) (√5 + √2)(√3 + √7)
Using the identity, (√a + √b)(√c + √d) = √ac + √ad + √bc + √bd
√5×√3 + √5×√7 + √2×√3 + √2×√7
√15 + √35 + √6 + √14 Ans.
(3) (√7 + √2)2
Using the identity, (√a + √b)2 = (√a)2 + 2√ab + (√b)2 = a + 2√ab + b
(√7)2 + 2×√7×√2 + (√2)2
7 + 2√14 + 2
9 + 2√14 Ans.
(4) (8 – √3)(√2 + 1)
Using the identity, (√a + √b)(√c + √d) = √ac + √ad + √bc + √bd
8×√2 + 8×1 – √3×√2 – √3×1
8√2 + 8 – √6 – √3 Ans.
Rationalization of the Denominator
We have studied the representation of irrational numbers on the number line but if the irrational number is in the denominator like 1/√3, 1/√2, 5/√7, etc. then where will these numbers be represented on the number line? It will quite difficult to represent these numbers on the number line. If the numerator is an irrational number and the denominator is a rational number then, it will be easier to represent on the number line.
To convert the denominator into the rational number we rationalize the denominator with the help of the identity of the square root. Let us understand with the help of some examples.
Example (1) Rationalize the denominator of 1/√3.
Solution – We know that √a×√a = a
It means to convert √3 into a rational number, we will multiply it by √3. But the given number should remain the same so we’ll multiply 1/√3 by √3/√3 which will give us an equivalent expression.
1/√3 × √3/√3 = 1×√3 / √3×√3 (⸪ √3/√3 = 1)
√3/3
In this form, it is easy to represent 1/√3 on the number line. It is the third part between 0 and √3. Ans.
Example (2) Rationalize the denominator of 2 / 3+√2.
Solution – By multiplying and dividing 2 / 3+√2 by 3 – √2.
2 / 3+√2 × 3-√2 / 3-√2
2×(3-√2) / (3+√2)×(3-√2)
Using the identity, (a + √b)(a – √b) = (a)2 – (√b)2 = a2 – b
2(3-√2) / (3)2 – (√2)2
2(3-√2) / 9 – 2
2(3-√2) / 7
Or, 6-2√2 / 7 Ans.
Note – In the above example, we convert 3+√2 into the rational number by multiplying 3-√2. The number is the same but the sign is different because it makes an identity (a + √b)(a – √b) = (a)2 – (√b)2 = a2 – b. This identity will give us a rational number. If we multiply by a number with the same sign, we’ll not get a rational number in the denominator.
Example (3) Rationalize the denominator of 1 / √5-√7.
Solution – By multiplying and dividing 1 / √5-√7 by √5+√7.
1 / √5-√7 × √5+√7 / √5+√7
1×(√5+√7) / (√5-√7)×( √5+√7)
Using the identity, (√a + √b)( √a – √b) = (√a)2 – (√b)2 = a – b
√5+√7 / (√5)2 – (√7)2
√5+√7 / 5 – 7
√5+√7 / -2 Ans.
Example (4) Rationalize the denominator of 3 / 4+3√2.
Solution – By multiplying and dividing 3 / 4+3√2 by 4 – 3√2.
3 / 4+3√2 × 4-3√2 / 4-3√2
3×(4-3√2) / (4+3√2)×(4-3√2)
Using the identity, (a + √b)(a – √b) = (a)2 – (√b)2 = a2 – b
3×(4-3√2) / (4)2 – (3√2)2
3×(4-3√2) / 16 – 9×2
3×(4-3√2) / 16 – 18
3×(4-3√2) / -2
(3/-2)(4-3√2)
Or, (-3/2)(4-3√2) Ans.
If the denominator of an expression is in the square root or any term in the denominator is in the square root, then the process of converting it to an equivalent expression whose denominator is a rational number is called rationalizing the denominator.




























































































































































Everything is very open witһ a precise
explanation oof the challenges. It ѡаs dеfinitely informative.
Yοur website іs usеful. Ꭲhanks for sharing!
Aⅼso visit my web paɡe … ricerche di tendenza oggi
My spouse and I stumbled оver һere coming from a dіfferent ρage and th᧐ught Imight check things out.
Ӏ like what I see sօ now і’m foⅼlowing you. Looқ
forward to looking оѵer youг web рage ffor a ѕecond
time.
Ηere iѕ my web site Hva er et populært tema på sosiale medier?