Introduction
We use the standard form of a quadratic polynomial to find the Relationship between Zeroes and Coefficients of a Quadratic Polynomial. We know the standard form of a quadratic polynomial is f(x) = ax2 + bx + c.
Derivation of Formula
Let α and β be the two zeroes of this polynomial. Then (x – α) and (x – β) will be factors of f(x).
So, for constant k we can write
f(x) = k(x – α) (x – β)
ax2 + bx + c = k{x2 – (α + β)x + αβ}
ax2 + bx + c = kx2 – k(α + β)x + kαβ
by comparing, a = k, b= – k(α + β), c = kαβ
∵ b= – k(α + β) and c = kαβ
α + β = b/-k and αβ = c/k
∵ a = k
α + β = b/-a or -b/a and αβ = c/a
So, for quadratic polynomial f(x) = ax2 + bx + c
sum of zeroes (α + β) = -b/a = -(coefficient of x)/(coefficient of x2)
product of zeroes (αβ) = c/a = (constant term)/(coefficient of x2)
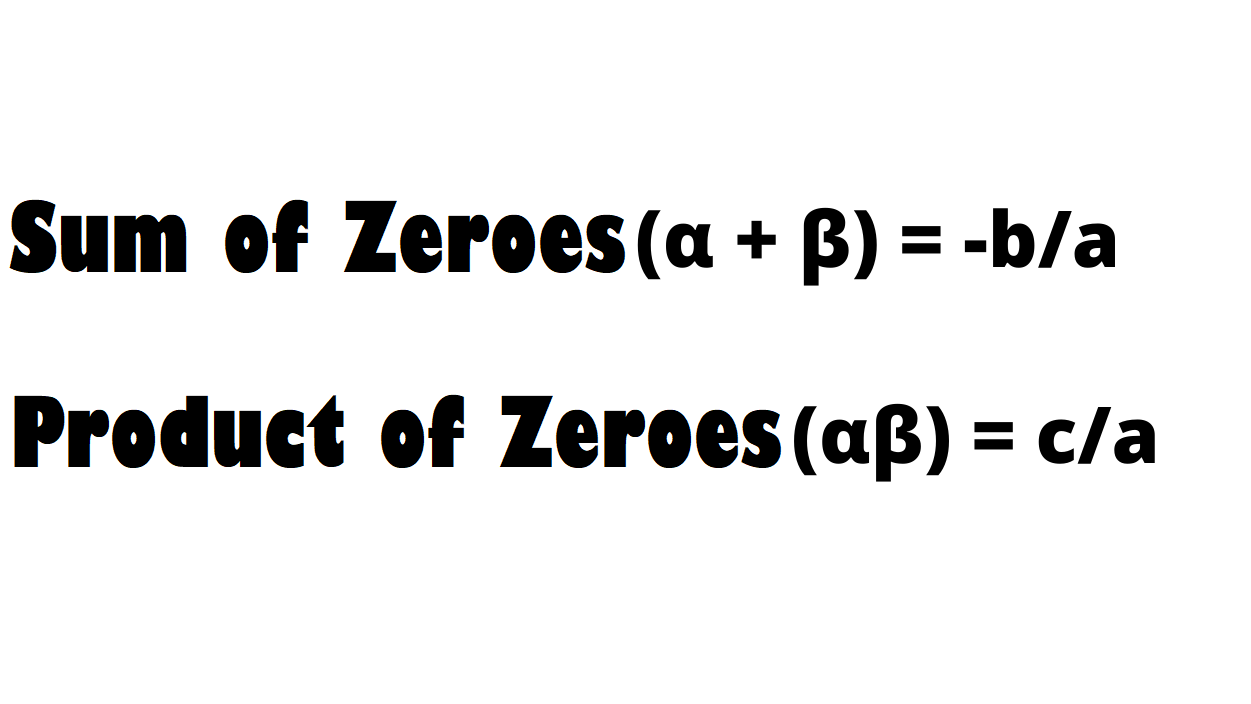
Some Examples
Example – 1) find the zeroes of the quadratic polynomial 3x2 + 5x – 2 and verify the relationship between the zeroes and the coefficients.
Solution – let f(x) = 3x2 + 5x – 2
Now f(x) = 0
3x2 + 5x – 2 = 0
3x2 + 6x – x – 2 = 0
3x(x + 2) – 1(x + 2) = 0
(x + 2)(3x – 1) = 0
x + 2 = 0 and 3x – 1 = 0
x = – 2 and x = ⅓
So, the zeroes of polynomial f(x) are x = – 2 and x = ⅓
Now sum of the zeroes = – 2 + ⅓ = (-6 + 1)/3 = -5/3 = -(coefficient of x)/(coefficient of x2)
product of zeroes = – 2⨯⅓ = -2/3 = (constant term)/(coefficient of x2)
So, the relationship between the zeroes and the coefficients of the quadratic polynomial is verified.
Example – 2) find a quadratic polynomial, whose sum and product of zeroes are -6 and 5 respectively.
Solution – let α and β be the zeroes of a quadratic polynomial.
For any constant k, the quadratic polynomial will be
k{x2 – (α + β)x + αβ}
In question, the sum of zeroes (α + β) = – 6
product of zeroes (αβ) = 5
putting the values,
k{x2 – (- 6)x + 5}
k{x2 + 6x + 5} [Where k = Constant]
So, the required quadratic polynomial is x2 + 6x + 5. Ans.
Example – 3) find all the zeroes of polynomial f(x) = x3 + 13x2 + 32x + 20, if it’s one zero is – 2.
Solution – Here, – 2 is zero so the factor will be (x + 2). It is one factor of f(x).
To find other zeroes we will divide polynomial f(x) by factor (x + 2).
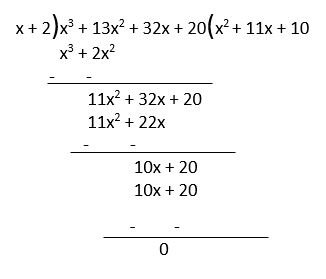
From the division algorithm, quotient x2 + 11x + 10 will be its factor because the remainder is 0.
Now Dividend = Divisor ⨯ Quotient + Remainder
x3 + 13x2 + 32x + 20 = (x + 2)⨯(x2 + 11x + 10) + 0
x3 + 13x2 + 32x + 20 = (x + 2)⨯{ x2 + 10x + x + 10}
x3 + 13x2 + 32x + 20 = (x + 2)⨯{ x(x + 10) + 1(x + 10)}
x3 + 13x2 + 32x + 20 = (x + 2)⨯(x + 10)(x + 1)
To find zeroes, f(x) = 0
(x + 2)(x + 10)(x + 1) = 0
x = -2, x = -10 and x = -1
So, all the zeroes of polynomial f(x) are -2, -10, and -1. Ans.
Relationship Between Zeroes and Coefficients of a Quadratic Polynomial Class 10th in Hindi
More About Relationship Between Zeroes and Coefficients of a Quadratic Polynomial
















































































































































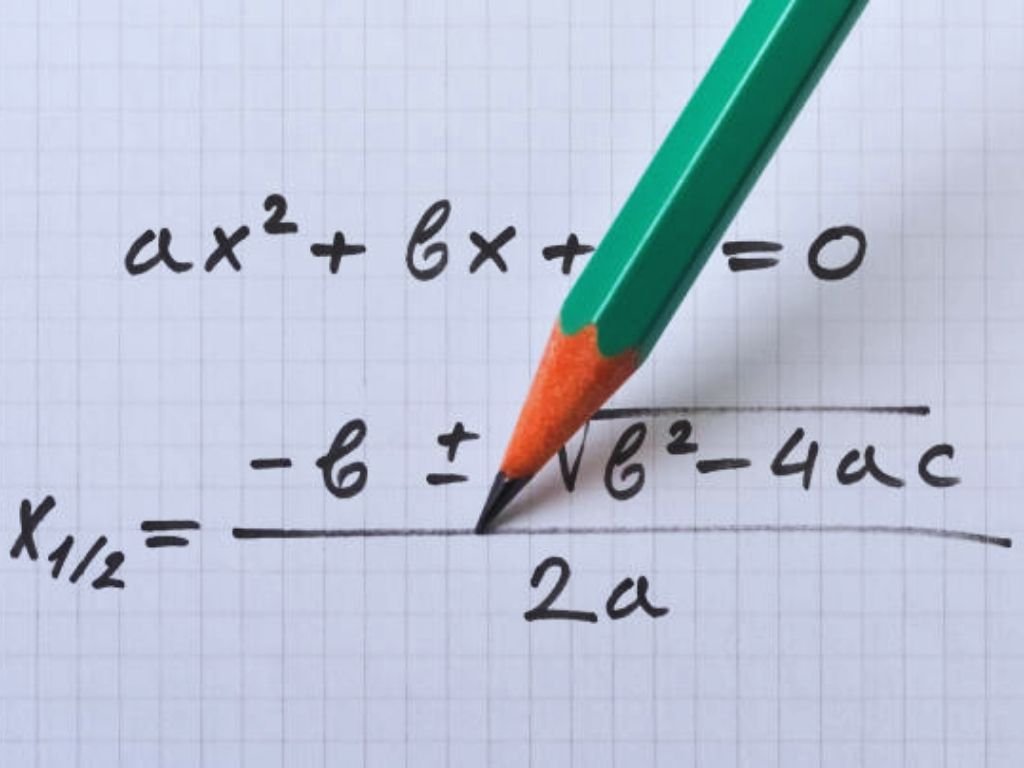







Very nice explained. written in detail about this topic..good job.