Trigonometric Ratios of Complementary Angles Class 10th

Introduction

When the sum of two angles is 90° they are called Complementary Angles. If any acute angle is A then its complementary angle will be (90° – A). In a Right-angled triangle, Trigonometric Ratios of Complementary Angles are found as follows.

Explanation

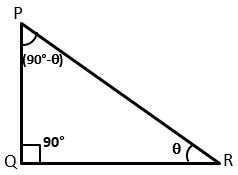
Let △PQR be a right-angled triangle in which ∠Q is the right angle and ∠R is the acute angle ϴ.

So, ∠P + ∠R = 90°

∠P + ϴ = 90°

∠P = (90° – ϴ)

Therefore ∠P and ∠R are complementary angles.

Now, trigonometric ratios for angle ϴ

sin ϴ = PQ/PR                 cos ϴ = QR/PR             tan ϴ = PQ/QR                 

cosec ϴ = PR/PQ             sec ϴ = PR/QR            cot ϴ = QR/PQ …………….(1)

Trigonometric ratios for angle (90° – ϴ)      

sin (90° – ϴ) = QR/PR              cos (90° – ϴ) = PQ/PR            tan (90° – ϴ) = QR/PQ               

cosec (90° – ϴ) = PR/QR          sec (90° – ϴ) = PR/PQ            cot (90° – ϴ) = PQ/QR …………..(2)

By comparing equations (1) and (2),

sin (90° – ϴ) = QR/PR = cos ϴ             cos (90° – ϴ) = PQ/PR = sin ϴ     

tan (90° – ϴ) = QR/PQ = cot ϴ                 cot (90° – ϴ) = PQ/QR = tan ϴ

cosec (90° – ϴ) = PR/QR = sec ϴ              sec (90° – ϴ) = PR/PQ = cosec ϴ

Therefore,

sin (90° – ϴ) = cos ϴ	cos (90° – ϴ) = sin ϴ
tan (90° – ϴ) = cot ϴ	cot (90° – ϴ) = tan ϴ
cosec (90° – ϴ) = sec ϴ	sec (90° – ϴ) = cosec ϴ

Note – It means sin and cos, tan and cot and cosec and sec are equal for complementary angles.

Some Examples –

Example – 1) Solve sin 35°/cos 55° 

Solution – ∵ 55° = 90° – 35°

∴ cos 55° = cos(90° – 35°)                    [∵ cos (90° – ϴ) = sin ϴ]

cos 55° = sin 35°

So,  sin 35°/sin 35° = 1        Ans.         

Example – 2) Solve cos² 50° + cos² 40°

Solution – ∵ 50° = 90° – 40°

∴ cos 50° = cos (90° – 40°) = sin 40°

And cos² 50° = sin² 40°

Therefore,    cos² 50° + cos² 40°

sin² 40° + cos² 40° = 1        [∵ sin² ϴ + cos² ϴ = 1] Ans.

Example – 3) Prove that tan 25° tan 55° tan 65° tan 35° = 1

Solution – LHS = tan 25° tan 55° tan 65° tan 35°

= tan (90° – 65°) tan (90° – 35°) tan 65° tan 35°

= cot 65° cot 35° tan 65° tan 35°

= 1/(tan 65° tan 35°) × tan 65° tan 35°

= 1

= RHS

Trigonometric Ratios of Complementary Angles Class 10^th in Hindi

More About Trigonometric Ratios of Complementary Angles